

APRESENTAÇÃO
Numa balança está um recipiente com água.
Uma esfera, suspensa por um fio, vai descendo com movimento uniforme controlado por um motor. Mergulha na água, atinge o fundo e de seguida sobe com movimento uniforme até sair completamente da água e finalmente pára. Durante o deslocamento da esfera, a balança marca uma possível variação do peso.
Em sua opinião:
A leitura da balança: não se altera? aumenta? ou diminui ?
EXPLICAÇÃO
A leitura da balança mantém-se constante até ao momento em que a esfera toca na superfície da água. Neste momento, alguma água sobe pela esfera, por acção da tensão superficial, provocando uma ligeira e temporária diminuição do peso marcado pela balança. Ao continuar a mergulhar, a esfera sofre uma força de impulsão que é igual ao peso do volume de água deslocado (princípio de Arquimedes). Pelo princípio da acção e da reacção a esfera exerce uma força igual (e oposta) sobre a água alterando a leitura da balança.
Assim o aumento de peso marcado pela balança é igual ao peso do líquido deslocado pela esfera ao entrar na água. Se a água deslocada saísse do vaso, a leitura da balança não se alteraria.
Pode calcular-se o peso do líquido deslocado através do cálculo do volume da esfera V ( z ) que está abaixo do nível da água, em que z é a distância do nível da água ao ponto mais baixo da esfera. Esta distância z está por sua vez relacionada com o deslocamento x da esfera, imposto pelo motor, o qual é proporcional ao tempo decorrido visto ser constante a velocidade do motor. Note-se que a relação ente x e z não é linear visto que z depende do nível da água que vai variando enquanto a esfera mergulha.
Desprezando os efeitos da tensão superficial que ocorrem quando a esfera está em contacto com a superfície da água, as equações que relacionam as várias grandezas envolvidas são:
![]()
![]()
em que a é o raio da esfera e R é o raio interno do vaso cilíndrico.
O volume de água deslocada V pode ser expresso em função de x e portanto em função do tempo t . As duas curvas simétricas representam o peso do volume de água deslocada V e foram obtidas por solução numérica das equações acima indicadas. O patamar superior do gráfico representa o peso da esfera. Os valores numéricos usados foram a =1,96 cm; R =5,49 cm, massa da esfera 79,6 g e massa específica da água 1g/cm 3 .
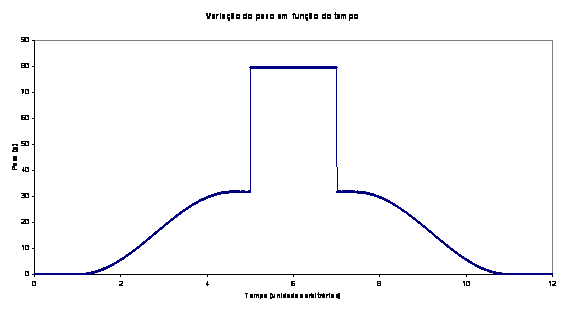
No gráfico que é traçado no decorrer da experiência pode ver-se claramente o efeito da tensão superficial no momento em que a esfera entra e sai da água. A leitura da balança mantém-se constante enquanto a esfera, totalmente mergulhada, vai descendo, mas aumenta bruscamente quando esta pousa no fundo do vaso.